• Exemplo: Cálculo do VIF no SAS
• Como lidar com a multicolinearidade

Na análise de regressão, a multicolinearidade ocorre quando duas ou mais variáveis preditoras estão altamente correlacionadas entre si, de tal forma que não fornecem informações únicas ou independentes no modelo de regressão.

Se o grau de correlação for suficientemente elevado entre as variáveis, pode causar problemas ao ajustar e interpretar o modelo de regressão.

Uma forma de detetar a multicolinearidade é através da utilização de uma métrica conhecida como fator de inflação da variância (VIF) que mede a correlação e a força da correlação entre as variáveis explicativas num modelo de regressão.

Este tutorial explica como calcular o VIF no SAS.

Exemplo: Cálculo do VIF no SAS

Para este exemplo, vamos criar um conjunto de dados que descreve os atributos de 10 jogadores de basquetebol:

 /*criar conjunto de dados*/ data my_data; input classificação pontos assistências ressaltos; datalines ; 90 25 5 11 85 20 7 8 82 14 7 10 88 16 8 6 94 27 5 6 90 20 7 9 76 12 6 6 75 15 9 10 87 14 9 10 86 19 5 7 ; run ; /*ver conjunto de dados*/ proc imprimir dados =my_data; 

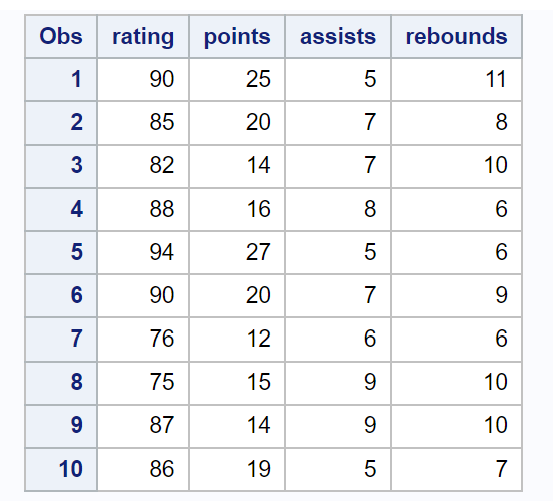
Suponha que gostaríamos de ajustar um modelo de regressão linear múltipla usando classificação como variável de resposta e pontos , assistências e ressaltos como variáveis de previsão.

Podemos utilizar o PROC REG para ajustar este modelo de regressão juntamente com o VIF para calcular os valores VIF para cada variável preditora no modelo:

 /*ajustar o modelo de regressão e calcular os valores VIF*/ proc reg data =my_data; model rating = pontos assistências ressaltos / vif ; run ; 

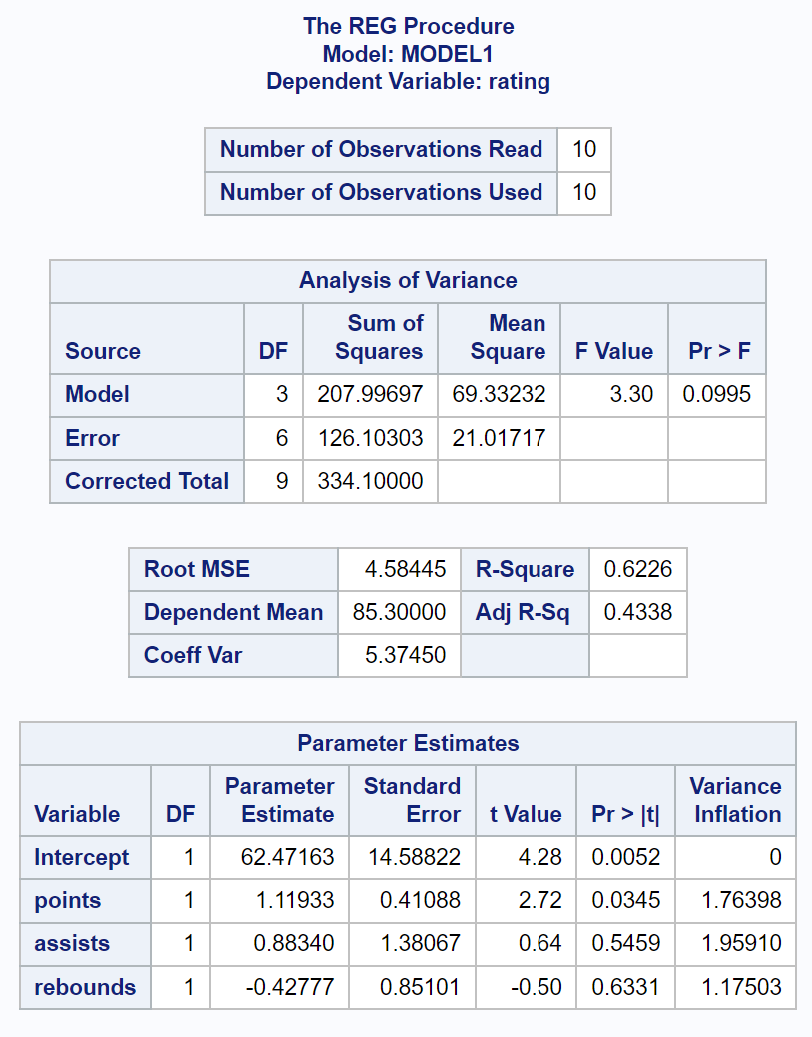
Do Estimativas de parâmetros podemos ver os valores VIF para cada uma das variáveis preditoras:

• pontos: 1.76398
• assistências: 1.96591
• rebotes: 1.17503

Nota: Ignorar o VIF para a "Interceção" no modelo, uma vez que este valor é irrelevante.

O valor de VIF começa em 1 e não tem limite superior. Uma regra geral para interpretar VIFs é a seguinte:

• Um valor de 1 indica que não existe correlação entre uma determinada variável preditora e quaisquer outras variáveis preditoras no modelo.
• Um valor entre 1 e 5 indica uma correlação moderada entre uma determinada variável preditora e outras variáveis preditoras no modelo, mas frequentemente não é suficientemente grave para exigir atenção.
• Um valor superior a 5 indica uma correlação potencialmente grave entre uma determinada variável preditora e outras variáveis preditoras no modelo. Neste caso, as estimativas do coeficiente e os valores p no resultado da regressão não são provavelmente fiáveis.

Dado que cada um dos valores VIF para as variáveis preditoras no nosso modelo de regressão está próximo de 1, a multicolinearidade não é um problema no nosso exemplo.

Como lidar com a multicolinearidade

Se determinar que a multicolinearidade é um problema no seu modelo de regressão, existem algumas formas comuns de o resolver:

1. remover uma ou mais das variáveis altamente correlacionadas.

Esta é a correção mais rápida na maioria dos casos e é frequentemente uma solução aceitável porque as variáveis que está a remover são redundantes e acrescentam pouca informação única ou independente ao modelo.

2) Combinar linearmente as variáveis preditoras de alguma forma, por exemplo, adicionando-as ou subtraindo-as de uma forma.

Ao fazê-lo, pode criar uma nova variável que engloba a informação de ambas as variáveis e deixa de ter um problema de multicolinearidade.

3. efetuar uma análise concebida para ter em conta variáveis altamente correlacionadas, como a análise de componentes principais ou a regressão por mínimos quadrados parciais (PLS).

Estas técnicas são especificamente concebidas para lidar com variáveis de previsão altamente correlacionadas.