- Exemplo 1: Interpretar um pequeno erro padrão de um declive de regressão
- Exemplo 2: Interpretar um erro padrão grande de um declive de regressão
O erro padrão do declive de uma regressão é uma forma de medir a "incerteza" na estimativa de um declive de regressão.
É calculado da seguinte forma:
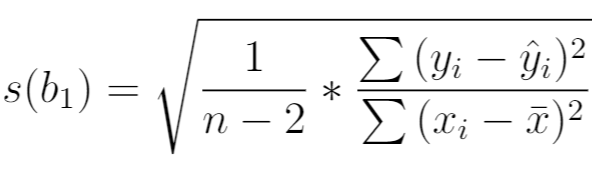
onde:
- n : dimensão total da amostra
- y i : valor efetivo da variável de resposta
- ŷ i : valor previsto da variável de resposta
- x i : valor efetivo da variável preditora
- x̄ : valor médio da variável preditora
Quanto mais pequeno for o erro padrão, menor será a variabilidade em torno da estimativa do coeficiente para o declive da regressão.
O erro padrão do declive da regressão será apresentado numa coluna de "erro padrão" no resultado da regressão da maioria dos programas estatísticos:
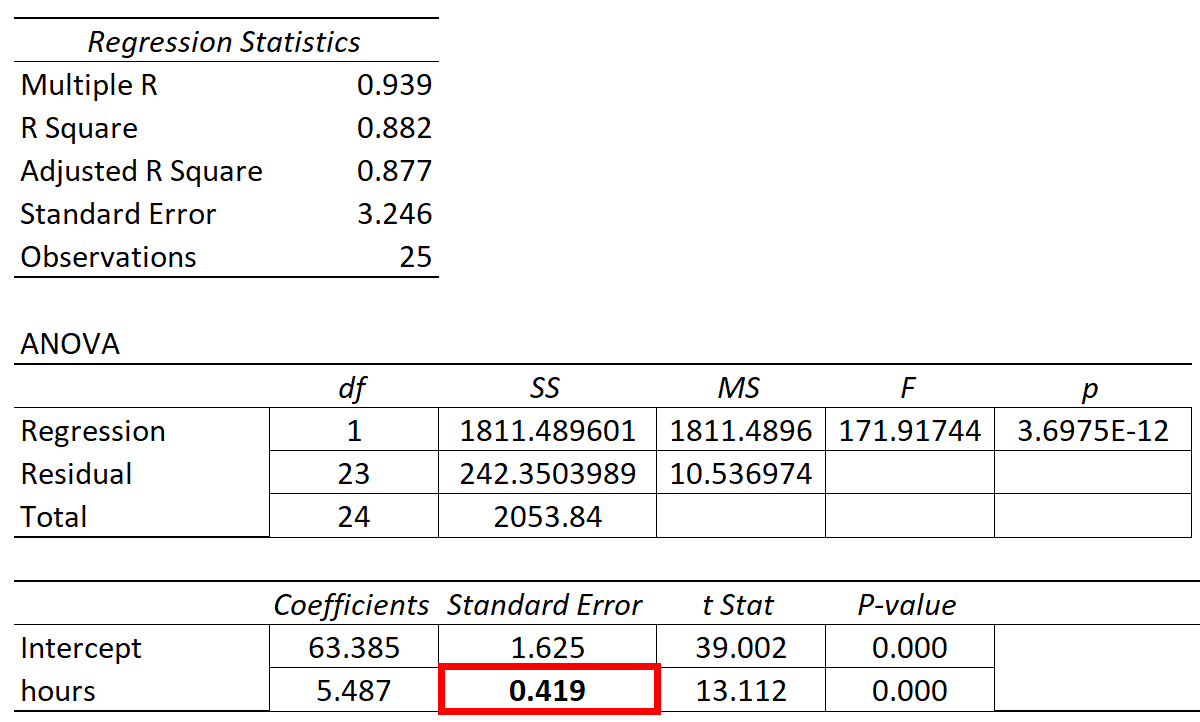
Os exemplos seguintes mostram como interpretar o erro padrão de um declive de regressão em dois cenários diferentes.
Exemplo 1: Interpretar um pequeno erro padrão de um declive de regressão
Suponha que um professor quer compreender a relação entre o número de horas estudadas e a nota do exame final recebida pelos alunos da sua turma.
Recolhe dados de 25 alunos e cria o seguinte gráfico de dispersão:
Existe uma clara associação positiva entre as duas variáveis: à medida que as horas de estudo aumentam, a pontuação no exame aumenta a um ritmo bastante previsível.
De seguida, ajusta um modelo de regressão linear simples utilizando as horas estudadas como variável preditora e a nota do exame final como variável de resposta.
O quadro seguinte apresenta os resultados da regressão:
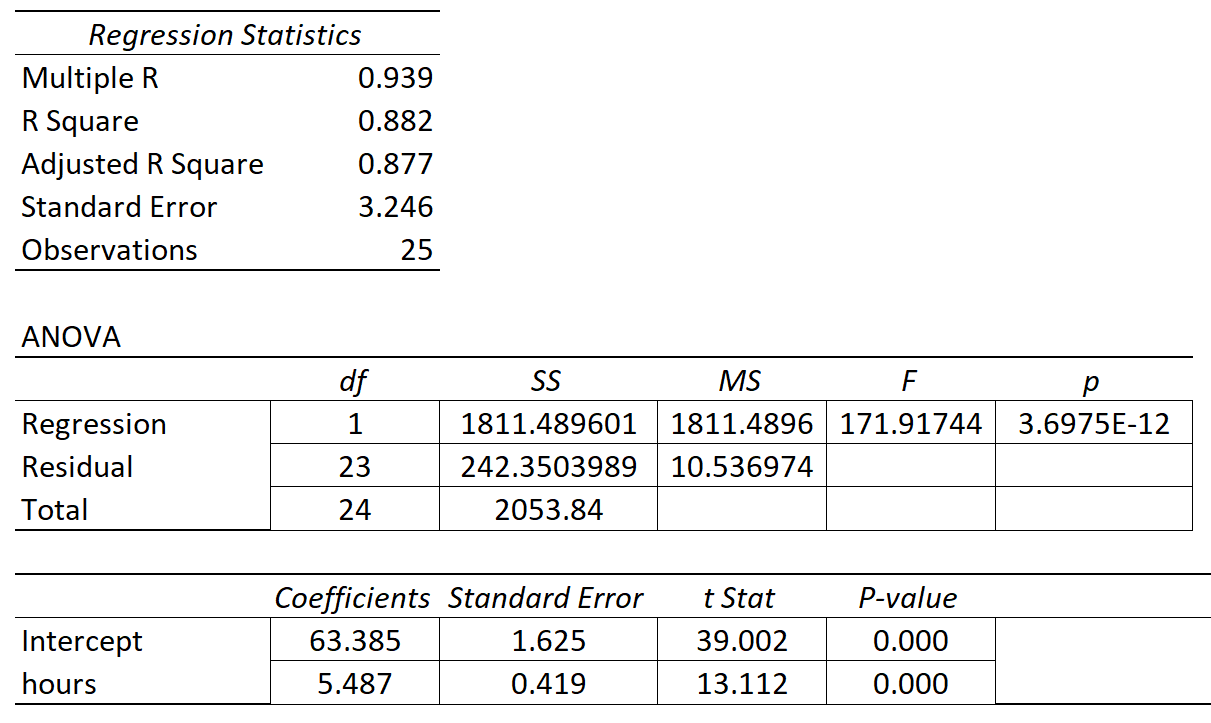
O coeficiente da variável preditora 'horas estudadas' é de 5,487, o que nos diz que cada hora adicional estudada está associada a um aumento médio de 5.487 na nota do exame.
O erro padrão é 0.419 que é uma medida da variabilidade em torno desta estimativa para o declive da regressão.
Podemos utilizar este valor para calcular a estatística t para a variável preditora "horas estudadas":
- Estatística t = estimativa do coeficiente / erro padrão
- Estatística t = 5,487 / .419
- Estatística t = 13,112
O valor de p que corresponde a esta estatística de teste é 0,000, o que indica que "horas estudadas" tem uma relação estatisticamente significativa com a nota do exame final.
Uma vez que o erro padrão da inclinação da regressão era pequeno em relação à estimativa do coeficiente da inclinação da regressão, a variável preditora era estatisticamente significativa.
Exemplo 2: Interpretar um erro padrão grande de um declive de regressão
Suponhamos que um outro professor quer compreender a relação entre o número de horas estudadas e a nota do exame final recebida pelos alunos da sua turma.
Recolhe dados de 25 alunos e cria o seguinte gráfico de dispersão:
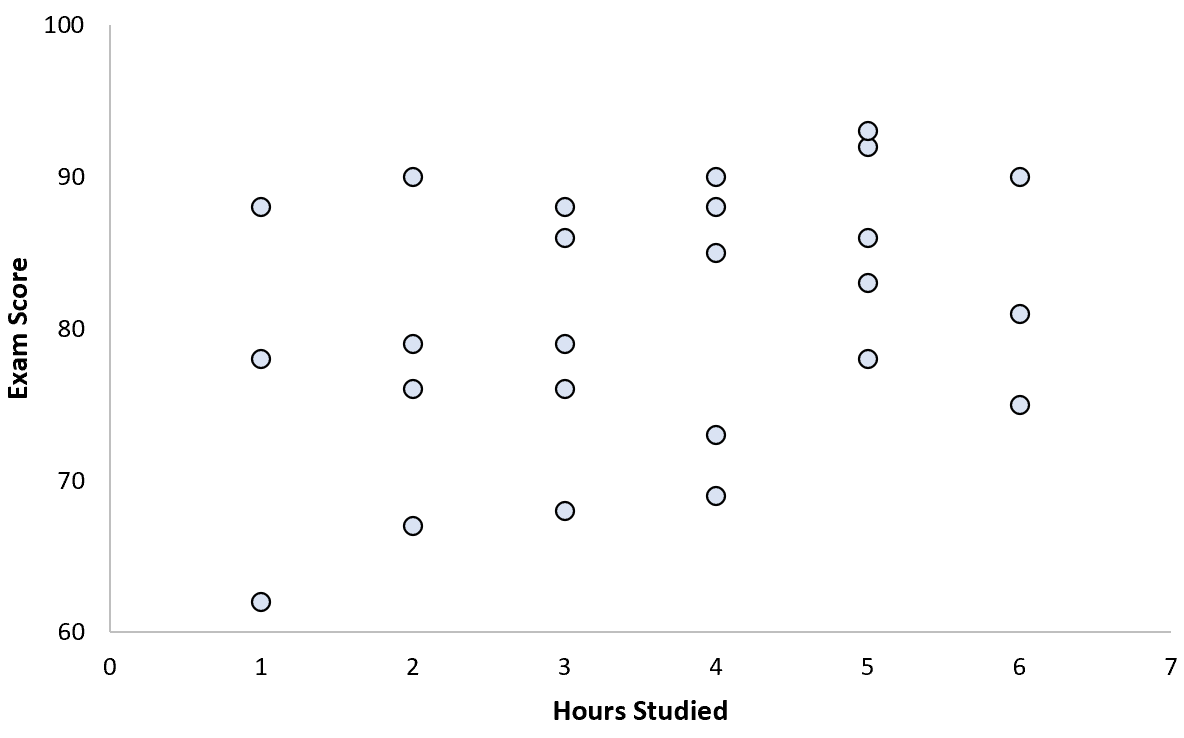
Parece haver uma ligeira associação positiva entre as duas variáveis: à medida que as horas de estudo aumentam, a nota do exame aumenta geralmente, mas não a um ritmo previsível.
Suponha que o professor ajusta um modelo de regressão linear simples usando as horas estudadas como variável preditora e a nota do exame final como variável de resposta.
O quadro seguinte apresenta os resultados da regressão:
O coeficiente da variável preditora 'horas estudadas' é de 1,7919, o que nos diz que cada hora adicional estudada está associada a um aumento médio de 1.7919 na nota do exame.
O erro padrão é 1.0675 que é uma medida da variabilidade em torno desta estimativa para o declive da regressão.
Podemos utilizar este valor para calcular a estatística t para a variável preditora "horas estudadas":
- Estatística t = estimativa do coeficiente / erro padrão
- Estatística t = 1,7919 / 1,0675
- Estatística t = 1,678
O valor de p que corresponde a esta estatística de teste é 0,107. Uma vez que este valor de p não é inferior a 0,05, isto indica que "horas estudadas" não tem uma relação estatisticamente significativa com a nota do exame final.
Como o erro padrão do declive da regressão era grande em relação à estimativa do coeficiente do declive da regressão, a variável preditora era não estatisticamente significativo.