• Exemplo: Calcular escores Z no SAS
• Como interpretar os escores Z no SAS

Em estatística, um escore z diz-nos a quantos desvios-padrão um valor se encontra da média.

Utilizamos a seguinte fórmula para calcular um z-score:

z = (X - μ) / σ

onde:

• X é um valor único de dados brutos
• μ é a média do conjunto de dados
• σ é o desvio padrão do conjunto de dados

O exemplo seguinte mostra como calcular os z-scores para valores de dados brutos no SAS.

Exemplo: Calcular escores Z no SAS

Suponhamos que criamos o seguinte conjunto de dados no SAS:

 /*criar conjunto de dados*/ dados dados_originais; valores de entrada; datalines ; 7 12 14 12 16 18 6 7 14 17 19 22 24 13 17 12 ; executar ; /*ver conjunto de dados*/ proc print dados =dados_originais; 

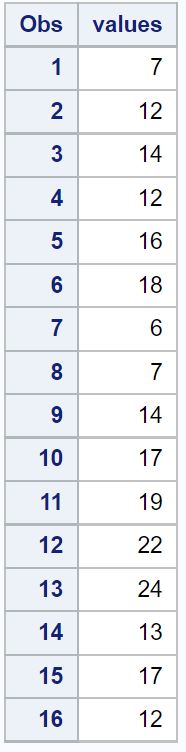
Agora, suponhamos que queremos calcular a pontuação z para cada valor no conjunto de dados.

Podemos utilizar proc sql para o fazer:

 /*criar uma nova variável que mostre as pontuações z para cada valor de dados brutos*/ proc sql ; select values, (values - mean(values)) / std(values) as z_scores from original_data; quit ; 

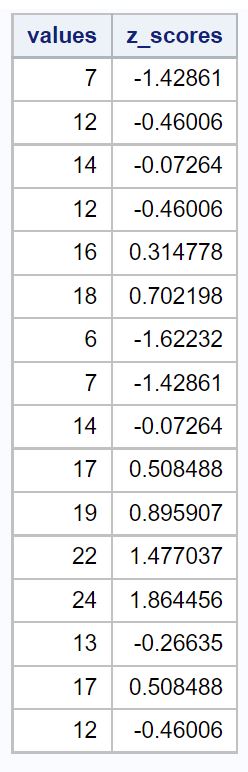
O valores apresenta os valores originais dos dados e a coluna z_escores mostra a pontuação z para cada valor.

Como interpretar os escores Z no SAS

A escore z diz-nos a quantos desvios-padrão um valor se encontra da média.

Um z-score pode ser positivo, negativo ou igual a zero.

Um z-score positivo indica que um determinado valor é superior à média, um z-score negativo indica que um determinado valor é inferior à média e um z-score de zero indica que um determinado valor é igual à média.

Se calculássemos a média e o desvio padrão do nosso conjunto de dados, verificaríamos que a média é 14.375 e o desvio padrão é 5.162 .

Assim, o primeiro valor no nosso conjunto de dados foi 7, que tinha um resultado z de (7-14,375) / 5,162 = -1.428 Isto significa que o valor "7" corresponde a 1,428 desvios-padrão abaixo a média.

O valor seguinte nos nossos dados, 12, tinha uma pontuação z de (12-14,375) / 5,162 = -0.46 Isto significa que o valor "12" corresponde a 0,46 desvios-padrão abaixo a média.

Quanto mais afastado um valor estiver da média, maior será o valor absoluto da pontuação z para esse valor.

Por exemplo, o valor 7 está mais afastado da média (14,375) do que o valor 12, o que explica o facto de o valor 7 ter um z-score com um valor absoluto maior.