• Exemplo: Interpretar resultados da ANOVA no SAS

Uma ANOVA unidirecional é utilizada para determinar se existe ou não uma diferença estatisticamente significativa entre as médias de três ou mais grupos independentes.

O exemplo seguinte mostra como interpretar os resultados de uma ANOVA unidirecional no SAS.

Exemplo: Interpretar resultados da ANOVA no SAS

Suponha que um investigador recruta 30 estudantes para participarem num estudo e que lhes é atribuído aleatoriamente um de três métodos de estudo para se prepararem para um exame.

Os resultados dos exames de cada aluno são apresentados a seguir:

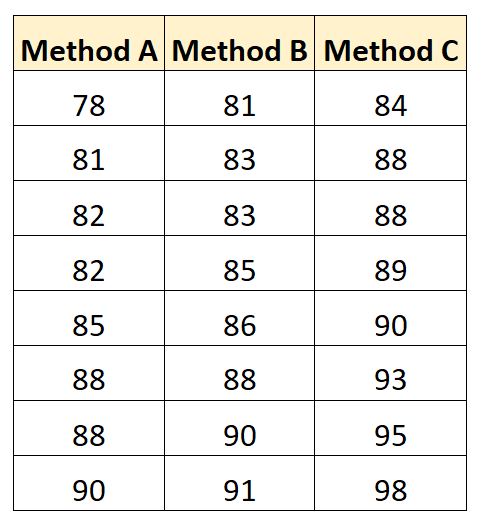
Podemos utilizar o seguinte código para criar este conjunto de dados no SAS:

 /*create dataset*/ data my_data; input Method $ Score; datalines ; A 78 A 81 A 82 A 82 A 82 A 85 A 88 A 88 A 90 B 81 B 83 B 83 B 85 B 86 B 88 B 90 B 91 C 84 C 88 C 88 C 89 C 90 C 93 C 95 C 98 ; run ; 

A seguir, utilizaremos proc ANOVA para efetuar a ANOVA unidirecional:

 /*executar ANOVA unidirecional*/ proc ANOVA data =my_data; class Method; model Score = Method; means Method / tukey cldiff ; run ; 

Nota : Utilizámos o meios juntamente com a declaração tukey e cldiff opções para especificar que deve ser efectuado um teste post-hoc de Tukey (com intervalos de confiança) se o valor p global da ANOVA unidirecional for estatisticamente significativo.

Primeiro, veremos a tabela ANOVA na saída:

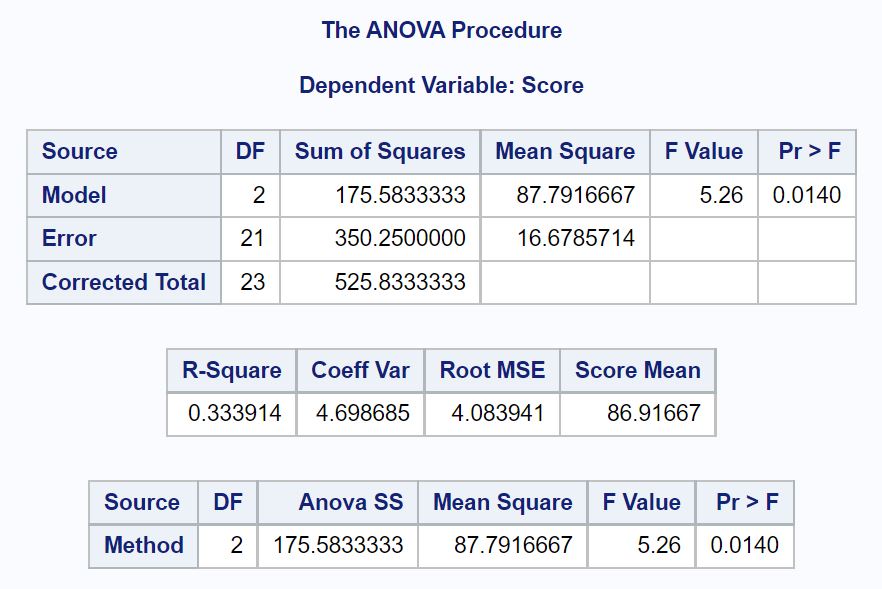
Eis como interpretar cada valor na saída:

Modelo DF: Os graus de liberdade da variável método Este valor é calculado como #grupos -1. Neste caso, havia 3 métodos de estudo diferentes, pelo que este valor é: 3-1 = 2 .

Erro DF: Os graus de liberdade para os resíduos, calculados como #total de observações - # grupos. Neste caso, havia 24 observações e 3 grupos, pelo que este valor é: 24-3 = 21 .

Total corrigido Soma do Modelo DF e do Erro DF: Este valor é 2 + 21 = 23 .

Modelo de Soma de Quadrados: A soma dos quadrados associada à variável método Este valor é 175.583 .

Soma dos erros quadrados: A soma dos quadrados associada aos resíduos ou "erros". Este valor é 350.25 .

Soma de quadrados corrigida Total Soma do modelo SS e do erro SS. Este valor é 525.833 .

Modelo de Quadrado Médio: A soma média dos quadrados associada a método Este valor é calculado como Modelo SS / Modelo DF, que é175,583 / 2 = 87.79 .

Erro quadrático médio: A soma média dos quadrados associada aos resíduos, calculada como Erro SS / Erro DF, que é 350,25 / 21 = 16.68 .

Valor F: A estatística F global do modelo ANOVA, que é calculada como o quadrado médio do modelo / erro quadrático médio, que é 87,79 / 16,68 = 5.26 .

Pr>F: O valor de p associado à estatística F com numerador df = 2 e denominador df = 21. Neste caso, o valor de p é 0.0140 .

O valor mais importante em todo o resultado é o valor p, porque nos diz se existe uma diferença significativa nos valores médios entre os três grupos.

Recorde-se que uma ANOVA unidirecional utiliza as seguintes hipóteses nula e alternativa:

• H ₀ (hipótese nula): Todas as médias dos grupos são iguais.
• H _A (hipótese alternativa): Pelo menos uma média de grupo é diferente das restantes.

Uma vez que o valor de p na nossa tabela ANOVA (0,0140) é inferior a 0,05, rejeitamos a hipótese nula.

Isto significa que temos provas suficientes para afirmar que a nota média do exame não é igual entre os três métodos de estudo.

Para determinar exatamente que médias de grupo são diferentes, temos de consultar a tabela final no output que mostra os resultados dos testes post-hoc de Tukey:

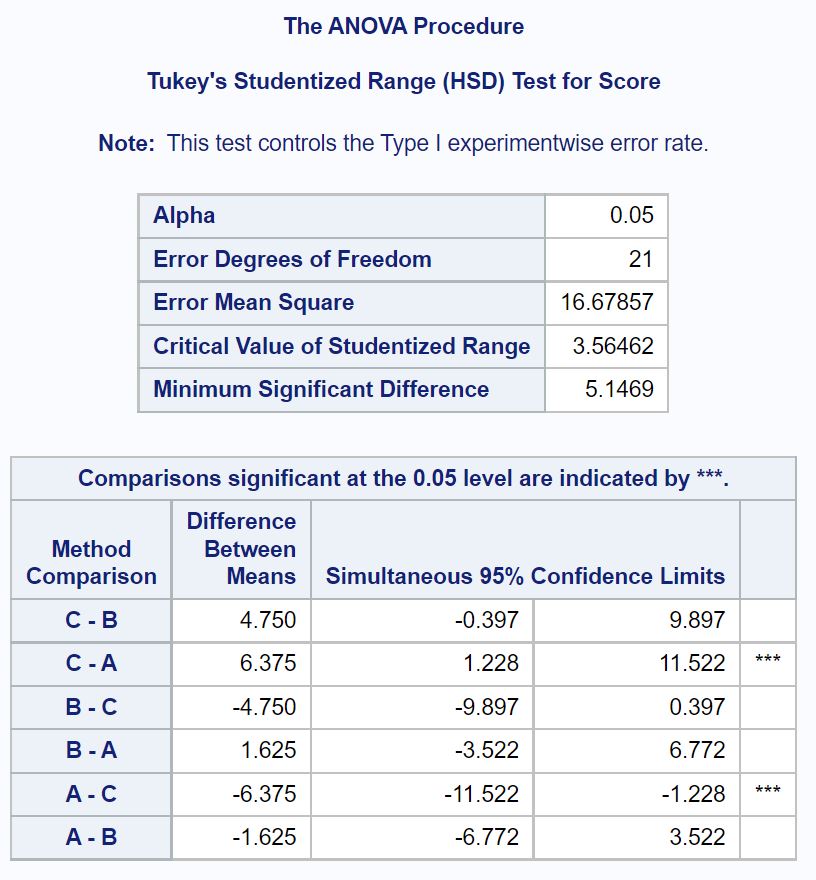
Para saber quais as médias dos grupos que são diferentes, temos de ver quais as comparações entre pares que têm estrelas ( *** ) ao seu lado.

A partir da tabela, podemos ver que existe uma diferença estatisticamente significativa nas classificações médias dos exames entre o grupo A e o grupo C.

Especificamente, a diferença média nas classificações dos exames entre o grupo C e o grupo A é 6.375 .

O intervalo de confiança de 95% para a diferença média é [1.228, 11.522] .

Não existem diferenças estatisticamente significativas entre as médias dos outros grupos.