• Exemplo: Classificação de variáveis quantitativas e amortecedoras; variáveis qualitativas
• Resumo da amostra quantitativa; variáveis qualitativas

Em estatística, existem dois tipos de variáveis:

1. Variáveis quantitativas: Por vezes designadas por variáveis "numéricas", são variáveis que representam uma quantidade mensurável, como por exemplo

• Número de alunos numa turma
• Número de metros quadrados de uma casa
• Dimensão da população de uma cidade
• Idade de um indivíduo
• Altura de um indivíduo

2. variáveis qualitativas: Por vezes designadas por variáveis "categóricas", são variáveis que assumem nomes ou rótulos e podem ser classificadas em categorias:

• Cor dos olhos (por exemplo, "azul", "verde", "castanho")
• Género (por exemplo, "masculino", "feminino")
• Raça do cão (por exemplo, "labrador", "bulldog", "poodle")
• Nível de ensino (por exemplo, "ensino secundário", "grau de associado", "grau de bacharel")
• Estado civil (por exemplo, "casado", "solteiro", "divorciado")

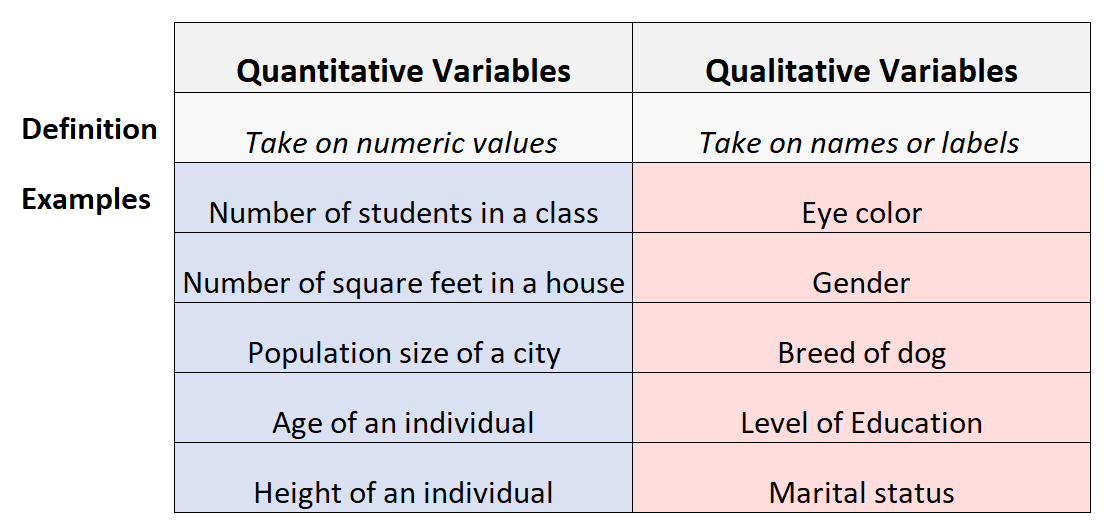
Todas as variáveis com que se depara em estatística podem ser classificadas como quantitativas ou qualitativas.

Exemplo: Classificação de variáveis quantitativas e amortecedoras; variáveis qualitativas

Considere o seguinte conjunto de dados com informações sobre 10 jogadores de basquetebol diferentes:

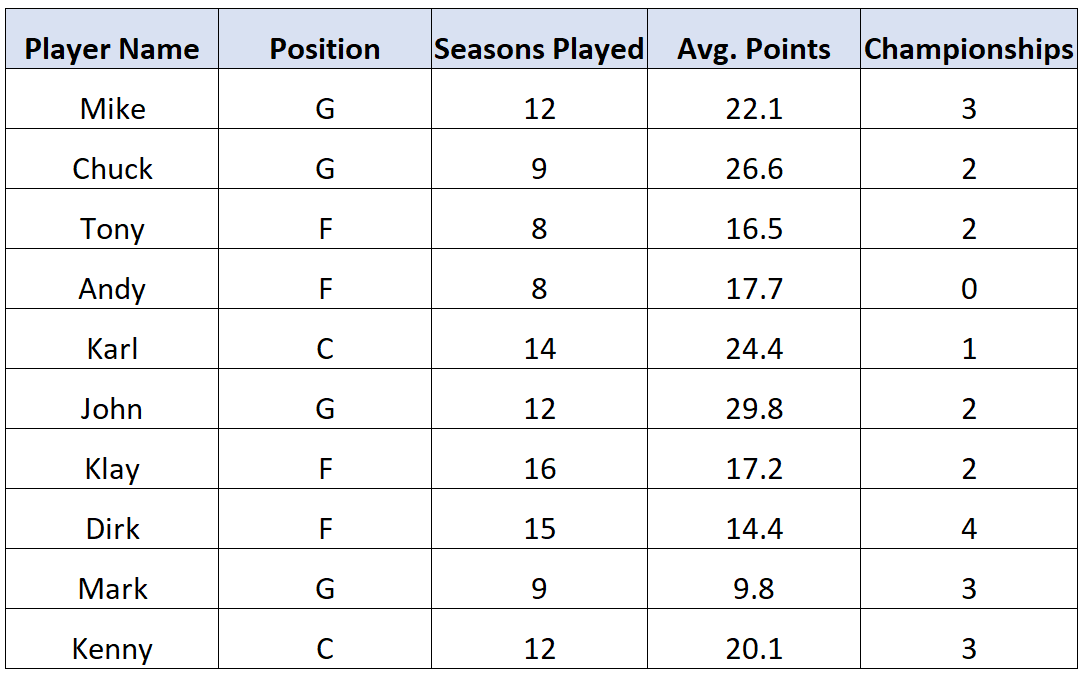
Há um total de cinco variáveis neste conjunto de dados, duas das quais são variáveis qualitativas e três são variáveis quantitativas:

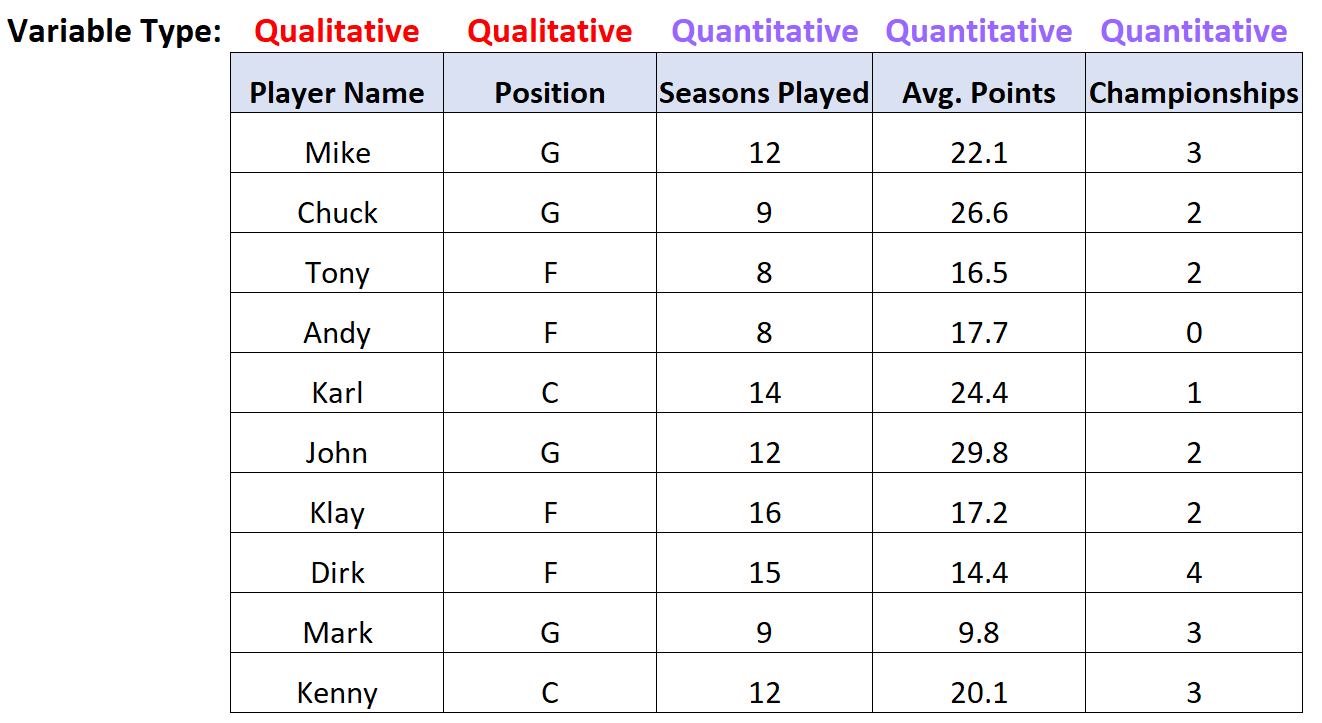
Resumo da amostra quantitativa; variáveis qualitativas

Podemos utilizar muitas métricas diferentes para resumir variáveis quantitativas , incluindo:

• Medidas de tendência central como a média, a mediana e a moda.
• Medidas de dispersão como a amplitude, a amplitude interquartil e o desvio padrão.

No entanto, só podemos utilizar tabelas de frequências e tabelas de frequências relativas para resumir variáveis qualitativas .

Para ilustrar este facto, consideremos mais uma vez o conjunto de dados do exemplo anterior:

Para a variável quantitativa Épocas jogadas podemos calcular as seguintes métricas:

• Média: 11.5
• Mediana: 12
• Modo: 12
• Alcance: 8
• Intervalo interquartil: 4.5
• Desvio padrão: 2.915

Estas métricas dão-nos uma boa ideia da localização do valor central, bem como da dispersão dos valores para esta variável.

E para a variável qualitativa Posição podemos criar uma tabela de frequências para descrever a frequência com que ocorrem valores diferentes:

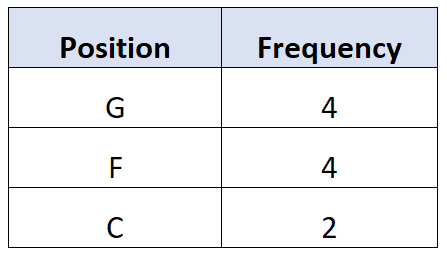
Esta tabela permite-nos ver rapidamente a frequência com que cada posição (G=guarda, F=avante, C=centro) ocorre no conjunto de dados.