ANCOVA Para compreender como funciona uma ANCOVA, é útil compreender primeiro a ANOVA.
Uma ANOVA (análise de variância) é utilizada para determinar se existe ou não uma diferença estatisticamente significativa entre as médias de três ou mais grupos independentes.
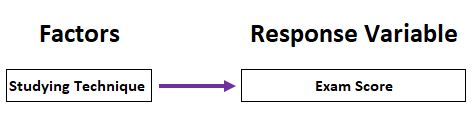
Por exemplo, suponhamos que queremos saber se a técnica de estudo tem ou não impacto nas notas dos exames de uma turma de alunos. Dividimos aleatoriamente a turma em três grupos. Cada grupo utiliza uma técnica de estudo diferente durante um mês para se preparar para um exame. No final do mês, todos os alunos fazem o mesmo exame.
Para descobrir se a técnica de estudo tem impacto nas classificações dos exames, podemos efetuar uma ANOVA unidirecional, que nos dirá se existe uma diferença estatisticamente significativa entre as classificações médias dos três grupos.
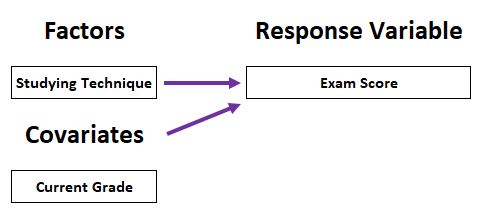
Um ANCOVA é uma extensão de uma ANOVA na qual gostaríamos de determinar se existe uma diferença estatisticamente significativa entre três ou mais grupos independentes após ter em conta uma ou mais covariáveis.
A covariável é uma variável contínua que varia em conjunto com a variável de resposta.
Por exemplo, suponhamos que queremos saber se a técnica de estudo tem ou não um impacto nas notas dos exames, mas queremos ter em conta a nota que o aluno já tem na turma Podemos utilizar a sua classificação atual como uma covariável e realizar uma ANCOVA para determinar se existe uma diferença estatisticamente significativa entre as classificações médias dos exames dos três grupos.
Isto permite-nos testar se a técnica de estudo tem ou não um impacto nas classificações dos exames depois de a influência da covariável ter sido removida.
Assim, se verificarmos que existe uma diferença estatisticamente significativa nas classificações dos exames entre as três técnicas de estudo, podemos ter a certeza de que essa diferença existe mesmo depois de ter em conta a nota atual do aluno na turma (ou seja, se ele já tem um bom desempenho ou não na turma) .
Pressupostos da ANCOVA
Antes de efetuar uma ANCOVA, é importante certificar-se de que os seguintes pressupostos são cumpridos:
- A(s) covariável(eis) e a(s) variável(eis) de fator são independentes - A covariável e a variável de fator devem ser independentes uma da outra, uma vez que adicionar um termo de covariável ao modelo só faz sentido se a covariável e a variável de fator actuarem independentemente na variável de resposta.
- A(s) covariável(eis) são dados contínuos. As covariáveis devem ser contínuas (ou seja, dados de intervalo ou de rácio).
- Homogeneidade das variâncias - As variâncias entre os grupos devem ser aproximadamente iguais.
- Independência - As observações de cada grupo devem ser independentes.
- Normalidade - Os dados devem ter uma distribuição aproximadamente normal em cada grupo.
- Sem valores anómalos extremos - Não deve haver valores extremos em nenhum dos grupos que possam afetar significativamente os resultados da ANCOVA.
ANCOVA: Exemplo
Um professor quer saber se três técnicas de estudo diferentes têm impacto nas notas dos exames, mas quer ter em conta a nota atual que o aluno já tem na turma.
Ela efectuará uma ANCOVA utilizando as seguintes variáveis:
- Variável de fator: técnica de estudo
- Covariável: grau atual
- Variável de resposta: nota do exame
O quadro seguinte apresenta o conjunto de dados relativos aos 15 alunos que foram recrutados para participar no estudo:
Depois de efetuar uma ANCOVA no conjunto de dados, o professor obtém os seguintes resultados:

O valor de p para a técnica de estudo é 0.03155 Como este valor é inferior a 0,05, podemos rejeitar a hipótese nula de que cada uma das técnicas de estudo conduz à mesma classificação média no exame, mesmo depois de ter em conta a classificação atual do aluno na turma .
Para determinar exatamente quais as técnicas de estudo que produzem diferentes resultados médios nos exames, o professor teria de realizar testes post-hoc.