• Regressão linear simples no Google Sheets
• Regressão linear múltipla no Google Sheets

Regressão linear é um método que pode ser utilizado para quantificar a relação entre uma ou mais variáveis explicativas e uma variável de resposta.

Utilizamos a regressão linear simples quando existe apenas uma variável explicativa e a regressão linear múltipla quando existem duas ou mais variáveis explicativas.

É possível efetuar ambos os tipos de regressões utilizando a função LINEST() no Google Sheets, que utiliza a seguinte sintaxe:

LINEST(dados_conhecidos_y, dados_conhecidos_x, calcular_b, verboso)

onde:

• dados_conhecidos_y: Conjunto de valores de resposta
• dados_conhecidos_x: Conjunto de valores explicativos
• calcular_b: Indica se deve ou não ser calculada a interceção y. Por defeito, esta opção é VERDADEIRA e é assim que a deixamos para a regressão linear.
• detalhado: Indica se deve ou não fornecer estatísticas de regressão adicionais para além do declive e da interceção. Por predefinição, esta opção é FALSA, mas iremos especificá-la como VERDADEIRA nos nossos exemplos.

Os exemplos seguintes mostram como utilizar esta função na prática.

Regressão linear simples no Google Sheets

Suponhamos que estamos interessados em compreender a relação entre horas estudadas e nota do exame. estuda para um exame e a nota que obtém no exame.

Para explorar esta relação, podemos efetuar uma regressão linear simples utilizando horas estudadas como variável explicativa e nota do exame como variável de resposta.

A seguinte captura de ecrã mostra como efetuar uma regressão linear simples utilizando um conjunto de dados de 20 alunos com a seguinte fórmula utilizada na célula D2:

= LINEST ( B2:B21 , A2:A21 , TRUE , TRUE )

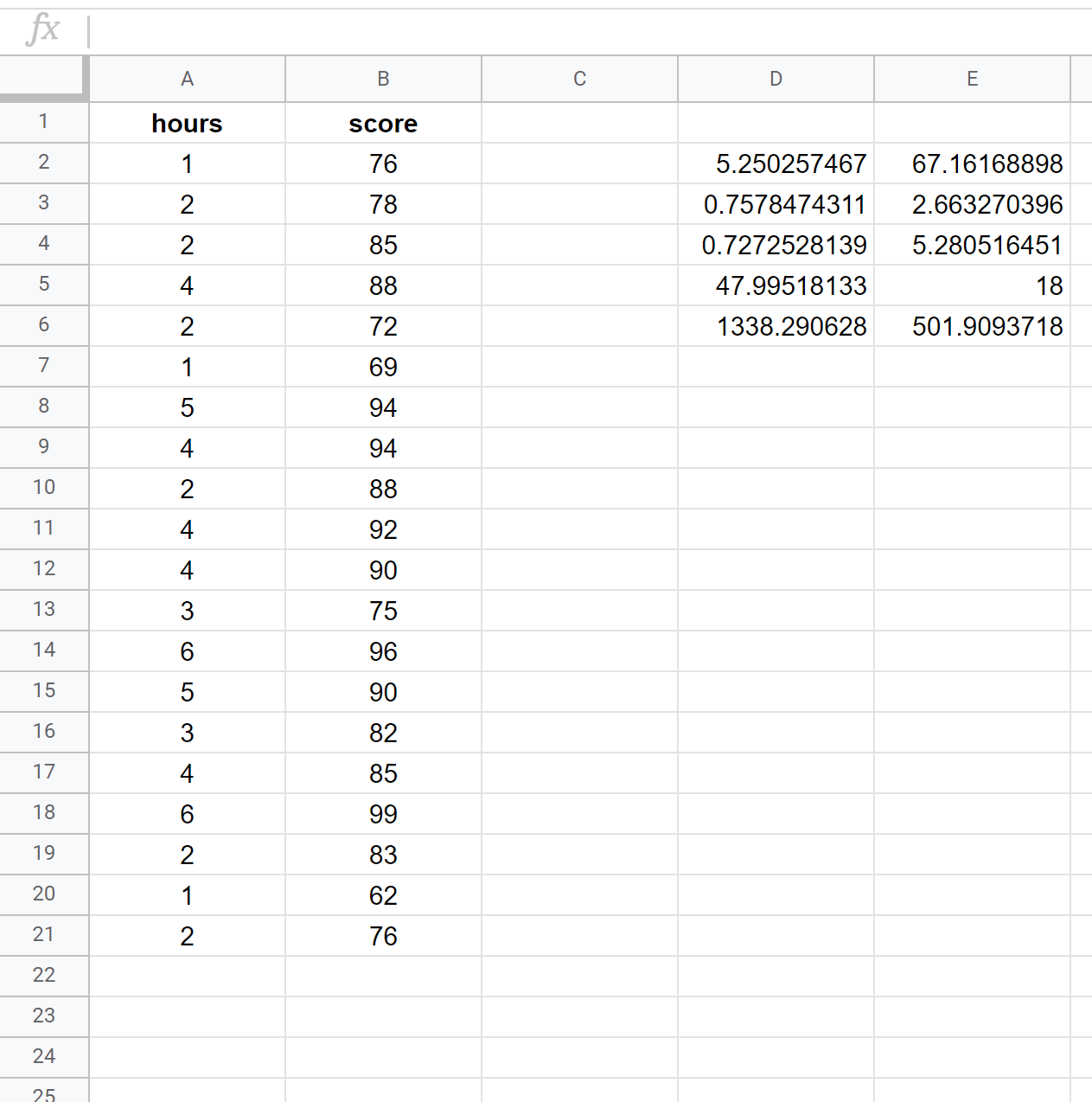
A seguinte captura de ecrã fornece anotações para a saída:

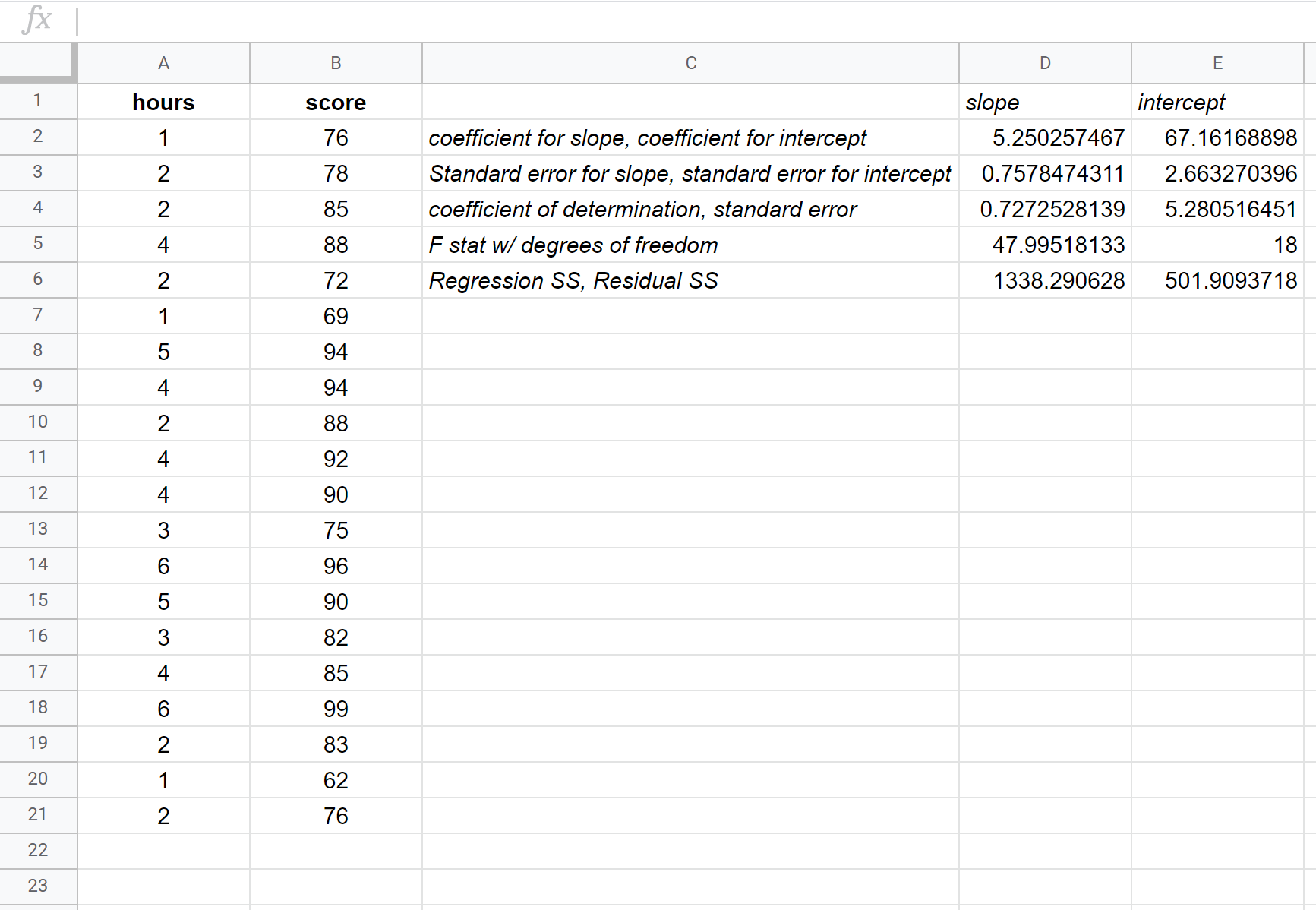
Eis como interpretar os números mais relevantes no resultado:

R Quadrado: 0.72725 É a proporção da variância na variável de resposta que pode ser explicada pela variável explicativa. Neste exemplo, cerca de 72,73% da variação nas notas do exame pode ser explicada pelo número de horas estudadas.

Erro padrão: 5.2805 É a distância média a que os valores observados se afastam da reta de regressão. Neste exemplo, os valores observados afastam-se em média 5,2805 unidades da reta de regressão.

Coeficientes: Os coeficientes dão-nos os números necessários para escrever a equação de regressão estimada. Neste exemplo, a equação de regressão estimada é

Nota do exame = 67,16 + 5,2503*(horas)

Interpretamos o coeficiente para as horas como significando que, por cada hora adicional estudada, se espera que a pontuação do exame aumente em 5.2503 Interpretamos o coeficiente para a interceção como significando que a nota de exame esperada para um aluno que estuda zero horas é 67.16 .

Podemos utilizar esta equação de regressão estimada para calcular a nota de exame esperada para um aluno, com base no número de horas que estuda. Por exemplo, espera-se que um aluno que estuda durante três horas receba uma nota de exame de 82.91 :

Nota do exame = 67,16 + 5,2503*(3) = 82,91

Regressão linear múltipla no Google Sheets

Suponhamos que queremos saber se o número de horas de estudo e o número de exames preparatórios efectuados afectam a pontuação que um aluno obtém num determinado exame de admissão à faculdade.

Para explorar esta relação, podemos efetuar uma regressão linear múltipla utilizando horas estudadas e exames preparatórios efectuados como variáveis explicativas e nota do exame como variável de resposta.

A seguinte captura de ecrã mostra como efetuar uma regressão linear múltipla utilizando um conjunto de dados de 20 alunos com a seguinte fórmula utilizada na célula E2:

= LINEST ( C2:C21 , A2:B21 , TRUE , TRUE )

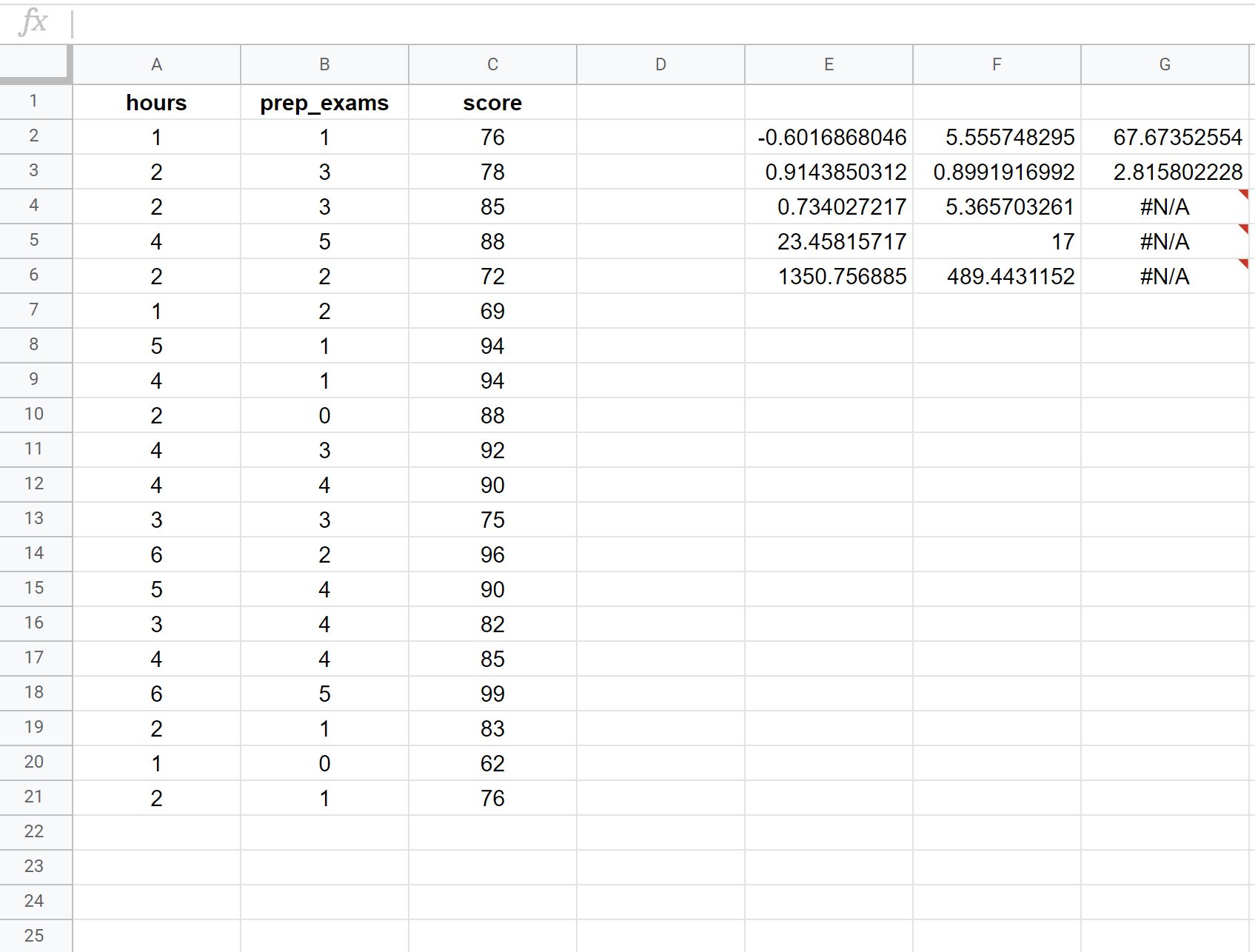
Eis como interpretar os números mais relevantes no resultado:

R Quadrado: 0.734 É a proporção da variância da variável de resposta que pode ser explicada pelas variáveis explicativas. Neste exemplo, 73,4% da variação nas classificações dos exames pode ser explicada pelo número de horas de estudo e pelo número de exames preparatórios efectuados.

Erro padrão: 5.3657 É a distância média a que os valores observados se afastam da reta de regressão. Neste exemplo, os valores observados afastam-se em média 5,3657 unidades da reta de regressão.

Equação de regressão estimada: Podemos utilizar os coeficientes do resultado do modelo para criar a seguinte equação de regressão estimada:

Nota do exame = 67,67 + 5,56*(horas) - 0,60*(exames preparatórios)

Podemos utilizar esta equação de regressão estimada para calcular a nota de exame esperada para um aluno, com base no número de horas que estuda e no número de exames de preparação que faz. Por exemplo, espera-se que um aluno que estuda durante três horas e faz um exame de preparação receba uma nota de 83.75 :

Nota do exame = 67,67 + 5,56*(3) - 0,60*(1) = 83,75