Regressão é um método estatístico que pode ser utilizado para determinar a relação entre uma ou mais variáveis de previsão e uma variável de resposta.
Regressão de Poisson é um tipo especial de regressão em que a variável de resposta consiste em "dados de contagem". Os exemplos seguintes ilustram casos em que a regressão de Poisson pode ser utilizada:
Exemplo 1: A regressão de Poisson pode ser utilizada para examinar o número de alunos que se formam num programa universitário específico com base nas suas classificações (GPA) à entrada no programa e no seu género. Neste caso, "número de alunos que se formam" é a variável de resposta, "GPA à entrada no programa" é uma variável de previsão contínua e "género" é uma variável de previsão categórica.
Exemplo 2: A regressão de Poisson pode ser utilizada para examinar o número de acidentes de viação num determinado cruzamento com base nas condições climatéricas ("sol", "nublado", "chuva") e na realização ou não de um evento especial na cidade ("sim" ou "não"). Neste caso, o "número de acidentes de viação" é a variável resposta, enquanto as "condições climatéricas" e o "evento especial" são variáveis preditoras categóricas.
Exemplo 3: A regressão de Poisson pode ser utilizada para examinar o número de pessoas à sua frente na fila de uma loja com base na hora do dia, no dia da semana e no facto de haver ou não uma venda ("sim" ou "não"). Neste caso, o "número de pessoas à sua frente na fila" é a variável resposta, a "hora do dia" e o "dia da semana" são variáveis preditoras contínuas e a "venda" é uma variável categóricavariável preditora.
Exemplo 4: A regressão de Poisson pode ser utilizada para examinar o número de pessoas que terminam um triatlo com base nas condições climatéricas ("soalheiro", "nublado", "chuvoso") e na dificuldade do percurso ("fácil", "moderado", "difícil"). Neste caso, o "número de pessoas que terminam" é a variável de resposta, enquanto as "condições climatéricas" e a "dificuldade do percurso" são variáveis preditoras categóricas.
A realização de uma regressão de Poisson permitir-lhe-á ver quais as variáveis preditoras (se existirem) que têm um efeito estatisticamente significativo na variável de resposta.
Para variáveis preditoras contínuas, será capaz de interpretar como um aumento ou diminuição de uma unidade nessa variável está associado a uma mudança percentual nas contagens da variável de resposta (por exemplo, "cada ponto adicional de aumento na GPA está associado a um aumento de 12,5% no número de alunos que se formam").
Para variáveis preditoras categóricas, será capaz de interpretar a alteração percentual nas contagens de um grupo (por exemplo, o número de pessoas que terminam um triatlo com tempo ensolarado) em comparação com outro grupo (por exemplo, o número de pessoas que terminam um triatlo com tempo chuvoso).
Pressupostos da Regressão de Poisson
Antes de podermos efetuar uma regressão de Poisson, temos de nos certificar de que os seguintes pressupostos são cumpridos para que os nossos resultados da regressão de Poisson sejam válidos:
Pressuposto 1: A variável de resposta consiste em dados de contagem. Na regressão linear tradicional, a variável de resposta é constituída por dados contínuos. No entanto, para utilizar a regressão de Poisson, a nossa variável de resposta tem de ser constituída por dados de contagem que incluam números inteiros de 0 ou mais (por exemplo, 0, 1, 2, 14, 34, 49, 200, etc.). A nossa variável de resposta não pode conter valores negativos.
Pressuposto 2: As observações são independentes. Cada observação no conjunto de dados deve ser independente uma da outra, o que significa que uma observação não deve ser capaz de fornecer qualquer informação sobre uma observação diferente.
Hipótese 3: A distribuição das contagens segue uma distribuição de Poisson. Como resultado, as contagens observadas e esperadas devem ser semelhantes. Uma forma simples de testar este facto é desenhar as contagens esperadas e observadas e ver se são semelhantes.
Hipótese 4: A média e a variância do modelo são iguais. Isto resulta do pressuposto de que a distribuição das contagens segue uma distribuição de Poisson. Para uma distribuição de Poisson, a variância tem o mesmo valor que a média. Se este pressuposto for satisfeito, então tem-se equidispersão No entanto, este pressuposto é frequentemente violado, uma vez que a sobredispersão é um problema comum.
Exemplo: Regressão de Poisson em R
Vamos agora analisar um exemplo de como efetuar a regressão de Poisson em R.
Antecedentes
Suponhamos que queremos saber quantas ofertas de bolsas de estudo recebe um jogador de basebol do liceu de um determinado concelho, com base na sua divisão escolar ("A", "B" ou "C") e na sua nota no exame de admissão à faculdade (medida de 0 a 100).
O código seguinte cria o conjunto de dados com que vamos trabalhar, que inclui dados sobre 100 jogadores de basebol:
#fazer este exemplo reproduzível set.seed(1) #criar conjunto de dados dados <- data.frame(ofertas = c(rep(0, 50), rep(1, 30), rep(2, 10), rep(3, 7), rep(4, 3)), divisão = sample(c("A", "B", "C"), 100, replace = TRUE), exame = c(runif(50, 60, 80), runif(30, 65, 95), runif(20, 75, 95))) Compreender os dados
Antes de ajustarmos efetivamente o modelo de regressão de Poisson a este conjunto de dados, podemos obter uma melhor compreensão dos dados visualizando as primeiras linhas do conjunto de dados e utilizando a função dplyr para executar algumas estatísticas resumidas:
#ver dimensões do conjunto de dados dim(dados) # 100 3 #ver as primeiras seis linhas do conjunto de dados head(dados) # oferece exame de divisão #1 0 A 73.09448 #2 0 B 67.06395 #3 0 B 65.40520 #4 0 C 79.85368 #5 0 A 72.66987 #6 0 C 64.26416 #ver resumo de cada variável no conjunto de dados summary(dados) # oferece exame de divisão # Min. :0.00 A:27 Min. :60.26 # 1º Qu.:0.00 B:38 1º Qu.:69.86 # Mediana :0.50 C:35 Mediana :75.08 # Média :0.83Média :76.43 # 3º Qu.:1.00 3º Qu.:82.87 # Máx. :4.00 Máx. :93.87 # ver a média da nota do exame por número de ofertas library(dplyr) data %>% group_by (ofertas) %>% summarise (mean_exam = mean(exam)) # Uma tabela: 5 x 2 # ofertas mean_exam # #1 0 70.0 #2 1 80.8 #3 2 86.8 #4 3 83.9 #5 4 87.9
A partir do resultado acima, podemos observar o seguinte:
- Existem 100 linhas e 3 colunas no conjunto de dados
- O número mínimo de ofertas recebidas por um jogador foi zero, o máximo foi quatro e a média foi 0,83.
- Neste conjunto de dados, há 27 jogadores da divisão "A", 38 jogadores da divisão "B" e 35 jogadores da divisão "C".
- A nota mínima do exame foi de 60,26, a máxima de 93,87 e a média de 76,43.
- Em geral, os jogadores que receberam mais ofertas de bolsas de estudo tiveram tendência a obter classificações mais elevadas nos exames (por exemplo, a classificação média nos exames dos jogadores que receberam 0 ofertas foi de 70,0 e a classificação média nos exames dos jogadores que receberam 4 ofertas foi de 87,9).
Também podemos criar um histograma para visualizar o número de ofertas recebidas pelos jogadores com base na divisão:
#carregar ggplot2 package library(ggplot2) #criar histograma ggplot(data, aes(offers, fill = division)) + geom_histogram(binwidth=.5, position="dodge")
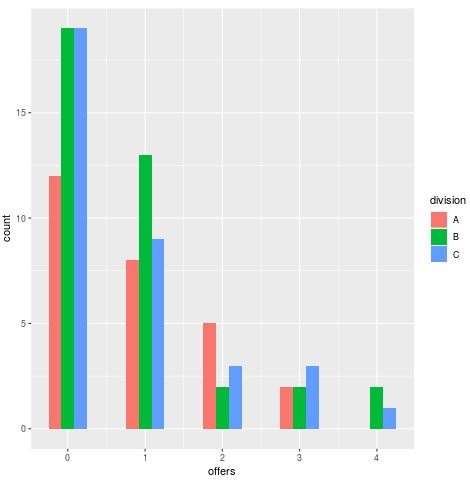
Podemos ver que a maioria dos jogadores recebeu zero ou uma oferta, o que é típico dos conjuntos de dados que seguem distribuições de Poisson: uma boa parte dos valores de resposta são zero.
Ajuste do modelo de regressão de Poisson
De seguida, podemos ajustar o modelo utilizando o glm() e especificando que gostaríamos de usar a função família = "poisson" para o modelo:
#ajustar o modelo modelo79,247 em 96 graus de liberdade #AIC: 204,12 # #Número de iterações da pontuação de Fisher: 5
A partir do resultado, podemos observar o seguinte:
- São fornecidos os coeficientes de regressão de Poisson, o erro padrão das estimativas, os valores z e os valores p correspondentes.
- O coeficiente para exame é 0.09548 o que indica que a contagem esperada do número de ofertas para um aumento de uma unidade em exame é 0.09548 Uma forma mais fácil de o interpretar é tomar o valor exponenciado, ou seja e0.09548 = 1.10 Isto significa que há um aumento de 10% no número de ofertas recebidas por cada ponto adicional obtido no exame de admissão.
- O coeficiente para divisãoB é 0.1756 o que indica que a contagem esperada do número de ofertas para um jogador na divisão B é 0.1756 mais elevado do que para um jogador da divisão A. Uma forma mais fácil de interpretar este facto é tomar o valor exponenciado, ou seja e0.1756 = 1.19 Isto significa que os jogadores da divisão B recebem mais 19% de ofertas do que os jogadores da divisão A. Note-se que esta diferença não é estatisticamente significativa (p = 0,519).
- O coeficiente para divisãoC é -0.05251 o que indica que a contagem esperada do número de ofertas para um jogador na divisão C é 0.05251 inferior do que para um jogador da divisão A. Uma forma mais fácil de interpretar este facto é tomar o valor exponenciado, ou seja e0.05251 = 0.94 Isto significa que os jogadores da divisão C recebem menos 6% de ofertas do que os jogadores da divisão A. Note-se que esta diferença não é estatisticamente significativa (p = 850).
A informação sobre o desvio do modelo também é fornecida. Estamos mais interessados na desvio residual que tem um valor de 79.247 sobre 96 Com estes números, podemos efetuar um teste de adequação do Qui-Quadrado para verificar se o modelo se ajusta aos dados. O código seguinte ilustra como efetuar este teste:
pchisq(79.24679, 96, lower.tail = FALSE) # 0.8922676
O valor de p para este teste é 0.89 Podemos concluir que os dados se ajustam razoavelmente bem ao modelo.
Visualização dos resultados
Também podemos criar um gráfico que mostre o número previsto de ofertas de bolsas de estudo recebidas com base na divisão e na pontuação do exame de admissão utilizando o seguinte código:
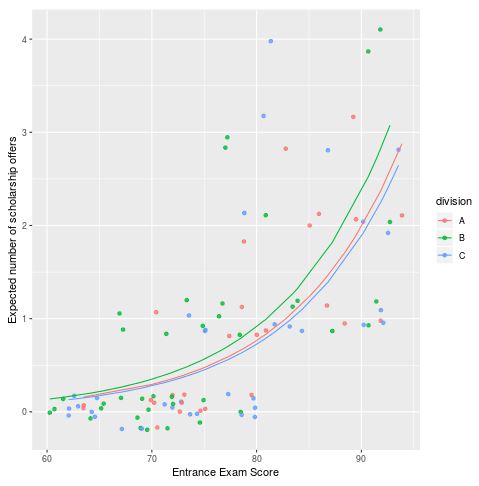
#encontrar o número previsto de ofertas utilizando o modelo de regressão de Poisson ajustado data$phat <- predict(model, type="response") #criar um gráfico que mostre o número de ofertas com base na divisão e na classificação do exame ggplot(data, aes(x = exam, y = phat, color = division)) + geom_point(aes(y = offers), alpha = .7, position = position_jitter(h = .2)) + geom_line() + labs(x = "Entrance Exam Score", y = "Expected numberde ofertas de bolsas de estudo")
O gráfico mostra o maior número de ofertas de bolsas de estudo esperadas para os jogadores que obtêm uma pontuação elevada no exame de admissão. Além disso, podemos ver que os jogadores da divisão B (a linha verde) deverão obter mais ofertas em geral do que os jogadores da divisão A ou da divisão C.
Comunicação dos resultados
Por último, podemos apresentar os resultados da regressão de uma forma que sintetize as nossas conclusões:
Foi efectuada uma regressão de Poisson para prever o número de ofertas de bolsas de estudo recebidas pelos jogadores de basebol com base nas classificações da divisão e do exame de admissão. Por cada ponto adicional obtido no exame de admissão, há um aumento de 10% no número de ofertas recebidas ( p <0,0001) . a divisão não foi considerada estatisticamente significativa.